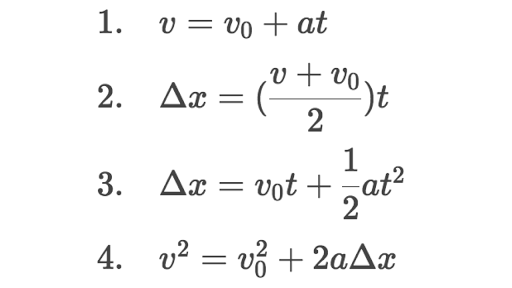The Kinematic Equations
How to describe 1D Motion
Kinematics
Kinematics deals with motion in a single dimension. Left to right, Up to down, something like that. While it may seem quite restricting right now (after all we live in 3 dimenstions), it’s important to be able to describe a single dimension before describing 3. Fundamentals are important in every field, and physics is no exception.
So in this post, I just want to review 4 key equations that are central to kinematics.
The Kinematic Equations
Below are the 4 essential equations to kinematics (assuming acceleration is constant):
Let’s go through each of them in order.
-
This is a pretty basic equation, and quite self-explanatory to say the least. The final velocity of an object is equal to the initial velocity plus the acceleration times time. Well, acceleration times time is just change in velocity. So, adding change in velocity to inital velocity is just final velocity.
-
This one’s a bit more complicated, but I’ll try to explain. Taking the average velocity (final plus initial over 2) and multiplying it by the time should yield displacement, because it’s similar to just rearranging the way to calculate area on a velocity graph. Just like how the formula for an arithmetic series works.
-
This equation is pretty complicated, but I think I have an idea. Initial velocity times time just represents the bottom rectangle under a velocity graph, while acceleration times time squared divided by 2 just represents the triangle above that (acceleration times time represents change in velocity or the vertical height between initial and final on the graph, time just represents the horizontal length).
-
I’m going to be honest, I don’t even know where to start on this one. I’ll probably figure it out later and edit this post. But for now, enjoy this picture of a sloth: