The Euclidean Algorithm

• Underlying Properties
• Example
• Implementation
• What's the Point?

Underlying Properties

I shamelessly pulled everything from this article

The Euclidean Algorithm takes advantages of two properties:

• GCD(A, 0) = A, GCD(0, B) = B
• Given that A = B * Q + R (B != 0, Q is an integer), then GCD(A, B) = GCD(B, R)

Explaining the first property is pretty simple. Since A is obviously the greatest divisor of itself, and 0 can divide any number, therefore GCD(A, 0) = A (and similarly for B).

Explaining the second property is more complicated. Suppose A - B = C.

First prove that GCD(A, B) evenly divides C.

A = X * GCD(A, B)

B = Y * GCD(A, B)

A - B = C

X GCD(A, B) - Y GCD(A, B) = C

(X - Y) * GCD(A, B) = C

Therefore GCD(A, B) evenly divides C.

Next, prove that GCD(B, C) evenly divides A.

A - B = C

B + C = A

M GCD(B, C) + N GCD(B, C) = A

(M + N) * GCD(B, C) = A

Therefore GCD(B, C) evenly divides A.

Next, prove that GCD(A, B) = GCD(A, A - B)

GCD(A, B) is given to evenly divide B. GCD(A, B) is proven to evenly divide C. Therefore, GCD(A, B) is a common divisor of B and C.

GCD(A, B) <= GCD(B, C) because GCD(B, C) is the greatest common divisor of B and C.

GCD(B, C) is given to divide B. GCD(B, C) is proven to divide A. Therefore, GCD(B, C) is a common divisor of A and B.

GCD(B, C) <= GCD(A, B) because GCD(A, B) is the greatest common divisor of A and B.

Since GCD(A, B) <= GCD(B, C) and GCD(B, C) <= GCD(A, B),

Therefore, GCD(A, B) = GCD(B, C).

A - B = C

GCD(A, B) = GCD(B, C)

GCD(A, B) = GCD(B, A - B)

Therefore, GCD(A, B) = GCD(B, A - B).

Summed up in this image: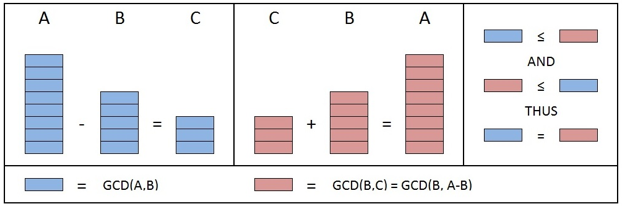

Finally, prove GCD(A, B) = GCD(B, R).

GCD(A, B) = GCD(B, A - B)

GCD(A, B) = GCD(A - B, B) (The order of the terms doesn't matter)

GCD(A, B) = GCD(A - B, B) = GCD(A - 2B, B) = GCD(A - 3B, B) = ... = GCD(A - Q * B, B) (Repeated application of property)

A = Q * B + R

R = A - Q * B

GCD(A, B) = GCD(R, B)

GCD (A, B) = GCD(B, R) (The order of the terms doesn't matter)

Example

Say you want to find the GCD of 147 and 91.

GCD(147, 91) = GCD(91, 147 % 91), and this can be applied multiple times over

147 % 91 = 56

GCD(91, 56) = GCD(56, 91 % 56)

91 % 56 = 35

GCD(56, 35) = GCD(35, 56 % 35)

56 % 35 = 21

GCD(35, 21) = GCD(21, 35 % 21)

35 % 21 = 14

GCD(21, 14) = GCD(14, 21 % 14)

21 % 14 = 7

GCD(14, 7) = GCD(7, 14 % 7)

14 % 7 = 0

GCD(7, 0) = 7

Therefore, the GCD of 147 and 91 is 7.

As you can see, repeatedly abusing the second property breaks down the huge number until reaching GCD(A, 0) or GCD(0, B), which easily simplifies to A or B respectively.

Implementation

Though the exact explanation is complicated, implementing it happens to be a lot more fun (and simple). I decided to utilize a recursory function to achieve this, taking the remainder over and over again until reaching 0, which would then return the GCD all the way back up.

public class EuclideanAlgorithm {

    public static int gcd(int a, int b) {
        if (b == 0) { // Final case of GCD(A, 0) = A
            return a;
        } else {
            return gcd(b, a % b); // Simplify the equation down
        }
    }

    public static void main(String[] args) {

        System.out.println(gcd(294, 182)); // Test case
    }
}

EuclideanAlgorithm.main(null);

14

What's the Point?

Basically this is useful for taking the modulus of super large numbers (combined with other modulus properties), which is utilized heavily in cryptography. It's also useful for determining if two numbers are coprime to one another, which can be used in more number theory related math. I might delve more into the math behind cryptography in the future, but stuff like this is good for now.